Special Theory 1905
General Theory 1916
These two ideas together are enough to require that we think of the universe as a 4-dimensional space-time in which the time between two events depends on who measures it, and whether two things happen at the same time depends on who's asking. Einstein's famous result that mass is a form of energy (E = mc2) also follows from these two fundamental principles, as does the result that no ordinary object can ever travel at a speed greater than the speed of light.
We can most easily understand a sequence of events by using a
space-time diagram. I'll use one
space dimension instead of 3, because I can't draw 4-D diagrams.
The diagram shows that there
is a limited region of space that we can know about: the region that
lies within our past light cone.
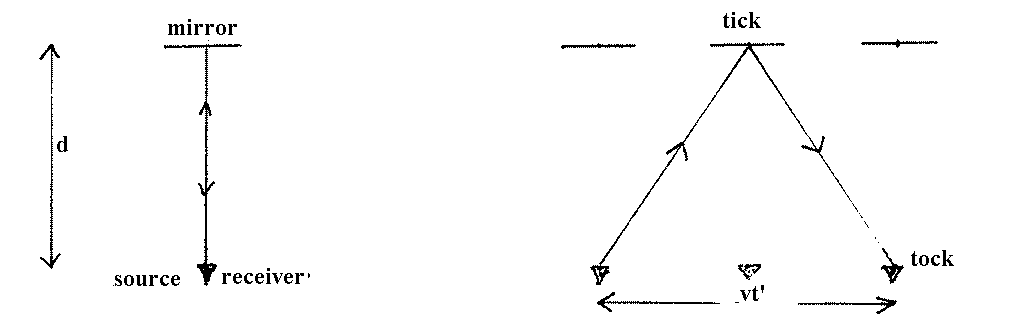
When the light hits the mirror it corresponds to "tick" and when it
return to the detector that
corresponds to "tock". Now consider two sets of observers, one set
remaining at rest with respect to the
clock and another set moving at speed v, as shown in the diagram. For
the first set of observers, the time
interval measured by the clock from sending the light flash to
receiving it again is t = 2d/c. The second
observers see a moving clock, and notice that the light must travel a
greater distance
Notice that t' > t. The shortest time interval between two events is always measured by an observer who sees the two events occur at the same place: it is called the proper time interval between the events. Your proper age is measured by your heartbeat: wherever you go. You always observe your heartbeat occuring at the same place: inside you. For anyone else, those heartbeats occur at different places, wherever you happen to be: inside the Humanities building; on the M-car; or at Fisherman's wharf.
Along with this time-dilation effect goes length contraction: l' = l × gamma
Nuclei can combine to form new nuclei, or can be split apart. Nuclear power plants use nuclear fission: Uranium is split up into lighter nuclei. Since the nuclei that emerge have a smaller total mass than the uranium, the mass difference is liberated as energy, according to Einstein's relation E = mc2.
The sun and the stars produce energy by nuclear fusion. Inside the
sun, hydrogen nuclei combine to
form helium. Since each helium nucleus has less mass than the 4
hydrogen nuclei that combine to
form it, the mass difference is liberated as energy in the form of
gamma
rays. By the time the gamma rays
work their way out to the solar surface, they have mostly degraded to
light and heat.
The mass of 1 hydrogen nucleus is 1.00797 atomic mass units (u).
The mass of 1 helium nucleus is 4.003 u.
Thus the mass difference per reaction is:
Quantum theory implies that the universe is an uncertain place. Empty space is not empty: energy can be borrowed for short periods of time to create particle/anti-particle pairs. These particles can then react with whatever else is around to form new particles. The temperature of the universe determines how much energy is available, on the average, to each particle, and thus determines the kinds of reactions that can occur. According to the big bang theory, the universe began as a very hot soup of elementary particles, and cooled down as it expanded. As the temperature drops, the rate at which particles react drops too, until the reaction rate is too slow to compete with the expansion of the universe, and reactions cease. We say that a certain kind of particle "freezes out" at a certain temperature. One major transition occured when the universe cooled to the point where free electrons and protons were replaced by neutral hydrogen atoms. This is analagous to the clearing of a fog, so that following this transition light could stream freely through the universe.
In his general theory of relativity, Einstein asserted that the fundamental reference frames for making measurements are those moving with objects that fall freely under the influence of gravity. Proceed- ing from this idea, he showed that space is curved, and that when mass is concentrated in a region it curves space in that region. Particles follow "straight lines" in this curved space, and we observe their motion as falling toward the massive object. In the same way, mass causes the whole universe to be curved. A closed universe is curved like a basketball, and will ultimately collapse back upon itself because of the gravitational attraction of the matter within it, forming a "big crunch": an open uni- verse contains less matter, is curved like a saddle, and will expand for ever. Exactly on the boudary between these two kinds of universe is the flat universe which is not curved at all.
Two fundamental riddles about the universe may have been solved by a new theory called "inflation". One is the horizon problem: given that the region of the universe we can know about (our "past") is so small, how can the universe be so uniform? The second is the flatness problem: we don't know whether the universe is open or closed, but we do know that it is not very far from flat in either direction. Since the parameter that measures flatness changes with time, we should not expect it to be so close to zero (meaning flat) right now, while we are alive.
The solution is that the universe underwent a dramatic change early on that caused a small region to expand rapidly. We live in this region which now appears both very uniform and very flat. This theory is closely linked to modern theories of the structure of matter on very small scales. It is not clear whether we will ever know if these theories are correct.