An ellipse is a curve which has the property that at any point on it, the sum of the distances from that point to each of two fixed points called the foci is a constant.
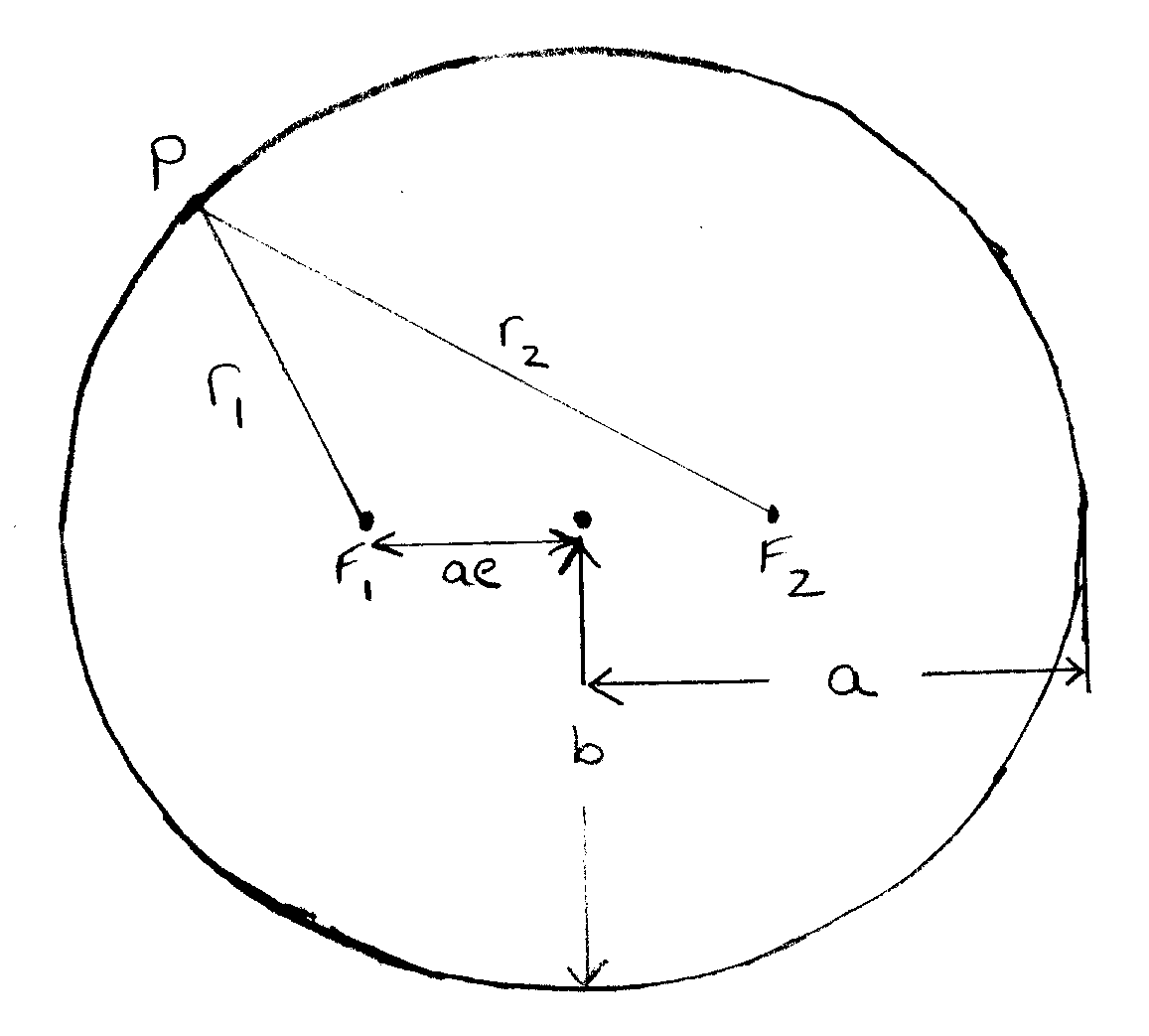In the diagram, r1 + r2 =
constant = 2a
The eccentricity of the ellipse measures its difference from a circle. The two foci are each distance ae from the geometrical center of the ellipse, and the semi-minor axis b is related to the semi-major axis a by:
Kepler didn't know why the planets moved in ellipses. Newton was the first to realise that if the sun pulls on each planet with a force which is proportional to 1/(distance)2, then the planet will move in an ellipse. Newton also realised that Kepler's 2nd law must hold if the force on each planet always points toward the sun.
As the diagram shows,
the force acting on the planet both changes its speed and the direction
of its
velocity. The planet moves fastest when it is closest to the sun, as
Kepler stated in his 2nd law.
Most planets have almost circular orbits ( e is very much less than 1). Data for the planets are given in the table below.
| Planet | Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus | Neptune | Pluto |
| Semi-major axis in AU |
0.387 | 0.723 | 1.00 | 1.524 | 5.203 | 9.54 | 19.18 | 30.06 | 39.44 |
| Period | 88 d | 224 d | 1.0 y | 1.88 y | 11.86 y | 29.46 y | 84.01 y | 164.8 y | 248.6 y |
| Eccentricity (e) | 0.21 | 0.007 | 0.017 | 0.093 | 0.048 | 0.056 | 0.047 | 0.009 | 0.249 |
Newtons law of gravity says that the force between two objects decreases as the inverse square of the distance between them: F = k/d2, where k is a constant. The brightness of a star also decreases as the inverse square of its distance from us. The same amount of light must pass through the surface of larger and larger spheres surrounding the star, spreading out over ever larger areas. The area of a sphere's surface is 4(pi)r2, where r is the radius of the sphere. The brightness of a star is the light energy per unit area falling on our eyes or on a photographic film, and thus B = L/r2, where L is a constant that depends on the kind of star.
It was argued that the universe could not be infinite because if it were, the sky would be infinitely bright. This is Olber's paradox . While named for Olber, it was probably first put forward by Kepler. If we consider a thin shell of the universe, distance r from us, the number of stars in that shell is the number n per unit volume (the density of stars) times the volume of the shell, which is its area times its thickness t: N = 4(pi)r2nt. The brightness of each star is B = L/r2. Thus the total brightness of the shell is:
number of stars x brightness of each star
L
= 4(pi)r2nt × --- = 4(pi)ntL, independent of r!
r2
Since each shell has the same brightness, and there are infinitely many shells in an infinite universe, the sky should be blindingly bright at night.
Well, it's not.
Why?
There are two answers.