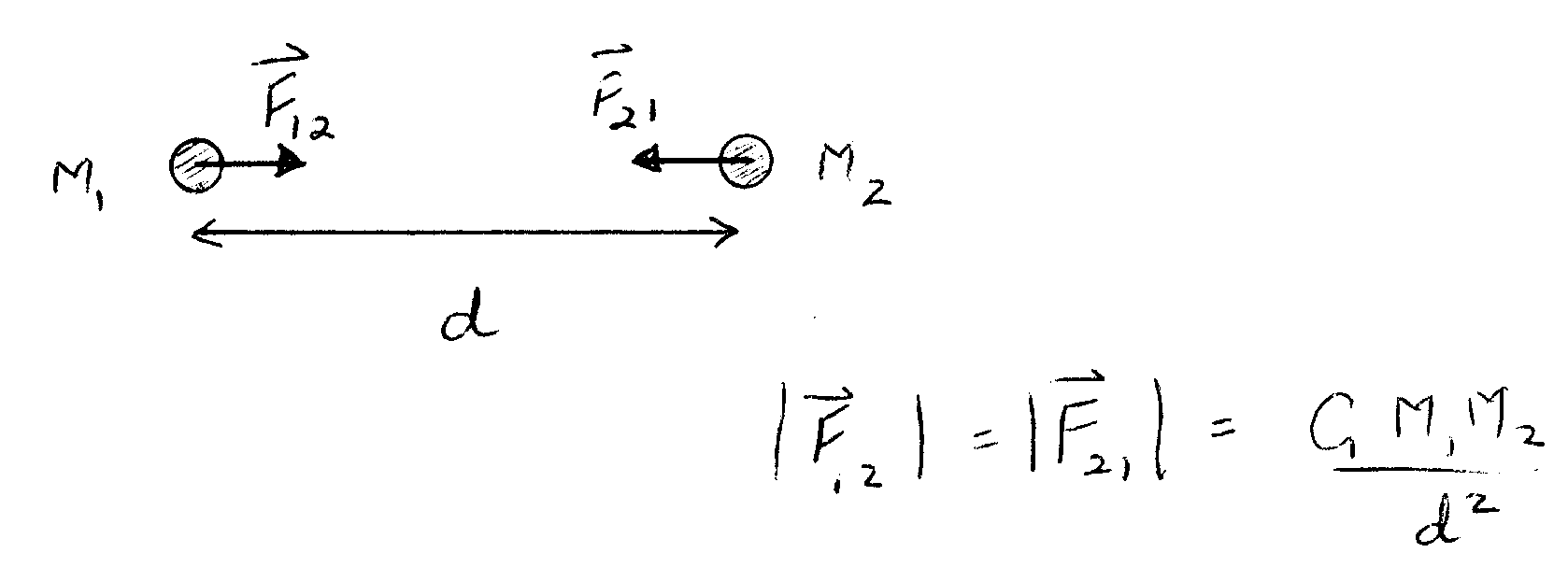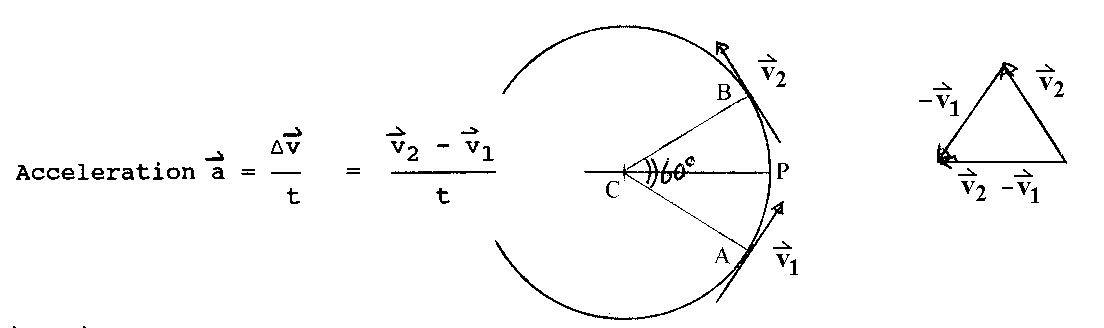VECTORS
Consider these two statements.
- The buried treasure is six feet away.
- The buried treasure is six feet away to the north.
The first tells you something about where the treasure is, but it would
take you quite a while to find it. The second statement tells you
exactly
where to dig!
The position of the treasure is described by its position
vector. The vector, represented by an arrow, tells you both the
distance and the direction of the treasure from you. Many physical
quantities have both size and direction, and so must be described by
vectors. Examples are velocity (whose size is just speed), acceleration
(rate of change of velocity) and magnetic field (as illustrated by a
compass needle).
The statement " I walked 3 miles north and then 4 miles west"
decscribes two vectors and the process of adding them. Where did you
end up? Draw a picture: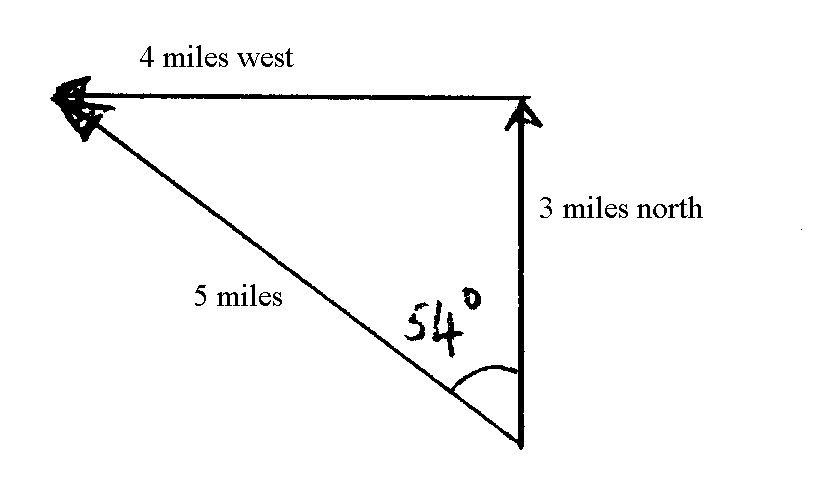
By Pythagoras
theorem, the length of the vector sum (the
third side of the triangle) is
square root(9+16) miles = square root(25) miles = 5 miles.
The direction is found by measuring off the triangle or by
trigonometry.
The answer is 53° 8' West of North.
To add any two vectors we place the tail of the second on the head of
the first and then draw a new vector from the tail of the first to the
head of the second, as in this diagram.
NEWTON'S LAWS
- A particle will remain at rest, or continue in uniform motion in
a
straight
line, unless acted upon by a force. (In common parlance, a force
is a push or a pull.)
- The acceleration of a body is proportional to the force exerted
on it:
F = ma,
where m is the mass of the body. - Because a force results from the interaction of two objects, forces
come in pairs. (For every
action there is an equal and
opposite
reaction.) The forces in the pair are equal in magnitude, opposite in
direction,
and act on different objects, the two objects that interact.
NEWTON'S LAW OF GRAVITY
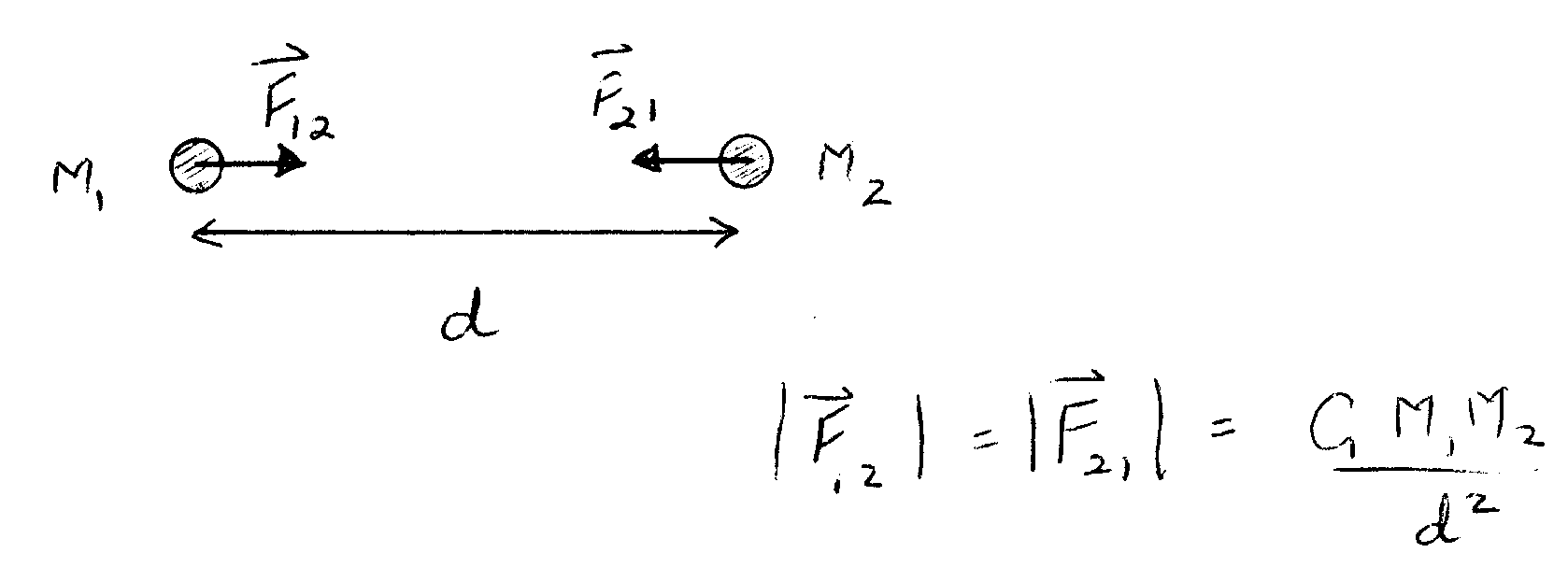
The gravitational force between two bodies is proportional to the
mass
of each body and inversely proportional to the square of the distance
between
their centers. The constant of proportionality G is the universal
gravitational
constant: G = 6.7x10-11 m3/kg.s2.
Newton (following ideas of Galileo and Descartes) reasoned that a body
in motion will continue to move at constant speed in a straight line
unless
acted upon by a force. Since circular motion is clearly not in a
straight
line, we need a force. If the circular motion occurs at constant speed,
the force acts only to change the direction of the velocity vector, and
not its length. Such a force acts at right angles to the velocity at
all
times, that is, towards the center of the circle.
Examples:
- A ball whirled around on the end of a string
- The force is provided by the string.
- The space shuttle in Earth orbit
- The force is provided by the Earth's gravity.
How much acceleration do we need? We can estimate the answer using a
diagram. Consider the change in velocity when a particle moves around
1/6 of a circle, i.e. through 60°.
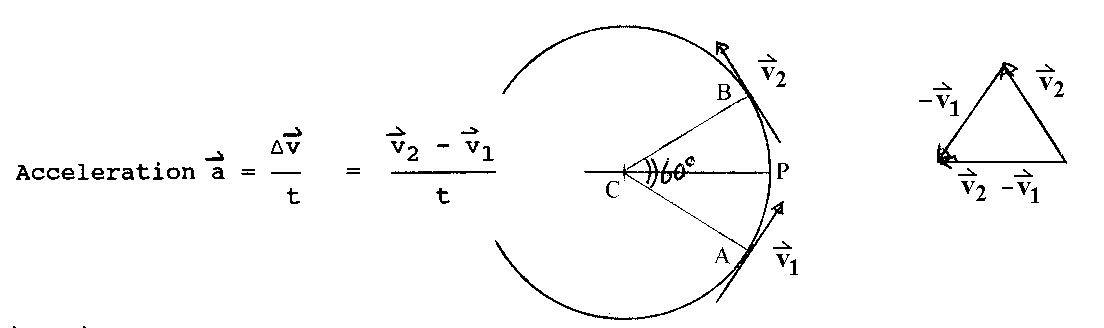
delta v v2 - v1
Acceleration a = ------- = -------
t t
v2 - v1 points towards the center
from
P, where P is halfway between A and B. From the drawing, the magnitude
of delta v = v = 2(pi)r/T. The time to achieve this change in
velocity
is 1/6 of the period, ie T/6. Thus the average acceleration during this
time has magnitude:
2(pi) 6 12(pi)
a = -----r - = ------r
T T T2
The exact answer, obtained using calculus, is (2pi)2/T2
times r. Our approximate answer is correct to within 5%. Thus the force
needed to make the particle move in a circle is mr(2pi/T)2.
USING NEWTON'S LAWS TO UNDERSTAND KEPLER'S
LAWS.
To make life easier, let's assume the planetary orbits are exactly
circular
instead of almost circular. (It makes the math easier, but doesn't
change
the result.) We know that the force required for circular motion is
mr(2pi/T)2.
If gravity provides this force, then:
Gmomp (2pi)2
F = ----- = mpr ------
r2 T2
where mo = mass of sun, mp = mass of the planet,
T = period, and r = radius of planet's orbit.
So: T2 = r3 (2pi)2/Gmo,
which is just Kepler's third law.