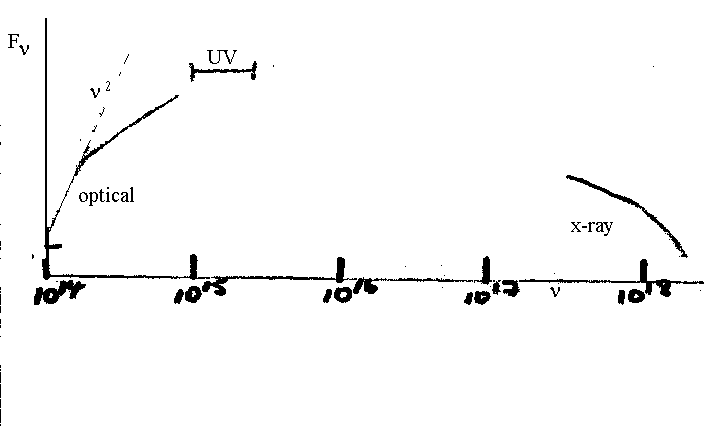
x-ray spectrum can be fit by a thermal bremsstrahlung spectrum with T = 7 x 107 K.
Fnu(1014 Hz) = 1.26 x 10-25 erg (cm2s.Hz)-1
Fnu(1015 Hz) = 1.5 x 10-24 erg (cm2s.Hz)-1
Fnu(3 keV) = 2 x 10-25 erg (cm2s.Hz)-1
Class schedule
| Date | Assignment due |
Topic | Book reference | ||
|---|---|---|---|---|---|
| R&L | Shu | Shore | |||
| Tu Jan 31 |
none | Radiation basics | 1.1-5 | Ch 1,2,3 | Ch 3 , 6.2.4,5 |
| Th Feb 2 |
#1 | Radiation basics |
1.1-5 |
||
| Tu Feb 7 | #2 | Einstein coefficients Scattering |
1.1-5 | Ch 1,2,3 | Ch 3 , 6.2.4,5 |
| Th Feb 9 |
Problem set 1 | Atmospheres | 1-6-8 | Ch 1,2,3 | Ch 3 , 6.2.4,5 |
| Tu Feb 14 |
#3 | Larmor formula for radiation by accelerating charges | Ch 2 | Ch 11-14 | Ch 3 , 6.2.4,5 |
| Th Feb 16 |
Bremsstrahlung, Thomson scattering | 3.1-4 | Ch 11-14 | Ch 3 , 6.2.4,5 §3.5.6 | |
| Tu Feb 21 | |
Line emission Line broadening; Curve of growth relevant link |
3.5-3.6 | Ch2 §1-30 | Ch 3 §3.3, 3.5.2-3.5.4 |
| ***** Paper topic statement due 2/21 ***** | |||||
| Th Feb 23 | Problem set 2 | Masers Fluorescence |
Ch 7 | Ch 14 | Ch3 §3.5.6 |
| Tu Feb 28 |
Compton
scattering Kompaneets equation |
Ch 7 | Ch 14 | ||
| Th Mar 2 |
Kompaneets equation | ||||
| Tu Mar 7 |
Synchrotron radiation | Ch 6 | |
Ch 6 § 6.5 Ch 7 § 7.7.2 |
|
| Th Mar 9 |
Problem set 3 | Fluids | Vol II Ch 1-4 |
Ch 1 § 1.4 Ch 1 § 1.5 Ch 4 § 4.2 |
|
| Tu Mar 14 |
Virial theorem |
VII Ch 8 | Ch 1 § 1.4.4 Ch 3 § 3.5.1 |
||
| Th Mar 16 |
Problem set 4 | Instabilities | |
V II Ch 15 | Ch 6 § 6.8, 9 |
| Tu Mar 21 |
Instabilities | ||||
| Th Mar 23 |
Shock waves | V II Ch 15 | Ch 6 § 6.7.1 Ch 6 § 6.7.5-6 |
||
| Tu Mar 28 |
Shock waves | |
|||
| ***** Abstract and outline due 3/28 ***** | |||||
| Th Mar 30 |
Ionization fronts | VII Ch 20 |
Ch 6 § 6.7.2-4 | ||
| Tu Apr 4-7 |
Spring Break |
|
|||
| Tu Apr 11 |
Problem Set 5 | Ionization fronts | |
||
| Th Apr 13 |
The two-body problem and binaries | V II Ch 6 | Ch 1 § 1.2.1 | ||
| Tu Apr 18 |
The two-body problem and binaries | ||||
| Th Apr 20 |
Problem set 6 | The three-body problem | V II Ch 6 | Ch 5 § 5.5-6 | |
| Tu Apr 25 |
Accretion and winds | Ch 3 § 3.7 | |||
| Th Apr 27 |
Accretion and winds | |
|||
| ****** First draft of paper due 4/27 ***** | |||||
| Tu May 2 |
Accretion and winds | ||||
| Th May 4 |
Advising Day |
||||
| Tu May 9 |
Accretion disks | V II Ch 7 | Ch 6 § 6.7.2-4 | ||
| Th May 11 |
A little cosmology | Ch 6 § 6.7.2-4 | |||
| ******* Second draft of paper due 5/11
********** |
|||||
| Tu May 16 |
A little cosmology | Ch 8 |
|||
| Th May 18 |
Student presentations Last day of classes |
|
|||
| **** Final paper due Tuesday 5/23 ***** | |||||
| Th May 25 |
Presentations continue | ||||
PROBLEM SET 3 Due Thursday March 9
R&L Problem 3.5
2. Scorpius X-1 is a very bright x-ray source which has a peculiar ("old-Nova-like") optical counterpart. A model has been developed for this source (eg Felton and Rees, 1972, A & A 17, 226) in which both the optical and x-ray emission emerge from the same cloud of ionized gas, which presumably surrounds and is heated by the central engine, whatever it might be. Use simple arguments based on the model described above, together with the data below, to estimate the size and density of the emitting cloud.
Data for Sco X-1 (See diagram)
x-ray spectrum can be fit by a thermal bremsstrahlung spectrum with
T = 7 x 107 K.
Fnu(1014 Hz) = 1.26 x 10-25 erg (cm2s.Hz)-1
Fnu(1015 Hz) = 1.5 x 10-24 erg (cm2s.Hz)-1
Fnu(3 keV) = 2 x 10-25 erg (cm2s.Hz)-1

PROBLEM SET 4 Due Thursday March 16th
R&L Problem 6.4
PROBLEM SET 5 Due Thursday April 11th
1. The velocity dispersion (measured in radial velocity) for the Coma Cluster is about 1000 km/s. (This is the rms velocity about the mean.) To apply the virial theorem to the cluster, we convert this to a 3-D velocity dispersion by multiplying by the square root of 3. (Explain why.) The effective radius of the cluster is Reff = 220', and the redshift of the cluster is vr= 6888 km/s. Assume that the gravitational energy of the cluster is just GM2/Reff . Estimate the total mass of the cluster. If the total luminosity is 1013 solar luminosities, calculate M/L in solar units. Comment on the results. How do your answers depend on the Hubble constant?
2. Investigate the stability of a plane interface between two fluids of densities rho1 and rho2 . Fluid 1 is moving with velocity v1 parallel to the boundary, and fluid 2 is moving with velocity v2 parallel to the boundary. Use perturbation methods to analyse the evolution of a small displacement of the boundary under the following assumptions:
PROBLEM SET 6 Due Thursday April 20th
Shu Volume I Problem Set 3 #1.